Import your data into R

1. Prepare your data as specified here: Best practices for preparing your data set for R

2. Save your data in an external .txt tab or .csv files

3. Import your data into R as follow:

# If .txt tab file, use this
my_data <- read.delim(file.choose())
# Or, if .csv file, use this
my_data <- read.csv(file.choose())

Here, we’ll use the built-in R data set named PlantGrowth. It contains the weight of plants obtained under a control and two different treatment conditions.

my_data <- PlantGrowth

Check your data

# print the head of the file
head(my_data)

  weight group
1   4.17  ctrl
2   5.58  ctrl
3   5.18  ctrl
4   6.11  ctrl
5   4.50  ctrl
6   4.61  ctrl

In R terminology, the column “group” is called factor and the different categories (“ctr”, “trt1”, “trt2”) are named factor levels. The levels are ordered alphabetically.

# Show the group levels
levels(my_data$group)

[1] "ctrl" "trt1" "trt2"

If the levels are not automatically in the correct order, re-order them as follow:

my_data$group <- ordered(my_data$group,
                         levels = c("ctrl", "trt1", "trt2"))

It’s possible to compute summary statistics by groups. The dplyr package can be used.

• To install dplyr package, type this:

install.packages("dplyr")

• Compute summary statistics by groups:

library(dplyr)
group_by(my_data, group) %>%
  summarise(
    count = n(),
    mean = mean(weight, na.rm = TRUE),
    sd = sd(weight, na.rm = TRUE),
    median = median(weight, na.rm = TRUE),
    IQR = IQR(weight, na.rm = TRUE)
  )

Source: local data frame [3 x 6]
   group count  mean        sd median    IQR
  (fctr) (int) (dbl)     (dbl)  (dbl)  (dbl)
1   ctrl    10 5.032 0.5830914  5.155 0.7425
2   trt1    10 4.661 0.7936757  4.550 0.6625
3   trt2    10 5.526 0.4425733  5.435 0.4675

Visualize the data using box plots

• To use R base graphs read this: R base graphs. Here, we’ll use the ggpubr R package for an easy ggplot2-based data visualization.

• Install the latest version of ggpubr from GitHub as follow (recommended):

# Install
if(!require(devtools)) install.packages("devtools")
devtools::install_github("kassambara/ggpubr")

• Or, install from CRAN as follow:

install.packages("ggpubr")

• Visualize your data with ggpubr:

# Box plots
# ++++++++++++++++++++
# Plot weight by group and color by group
library("ggpubr")
ggboxplot(my_data, x = "group", y = "weight", 
          color = "group", palette = c("#00AFBB", "#E7B800", "#FC4E07"),
          order = c("ctrl", "trt1", "trt2"),
          ylab = "Weight", xlab = "Treatment")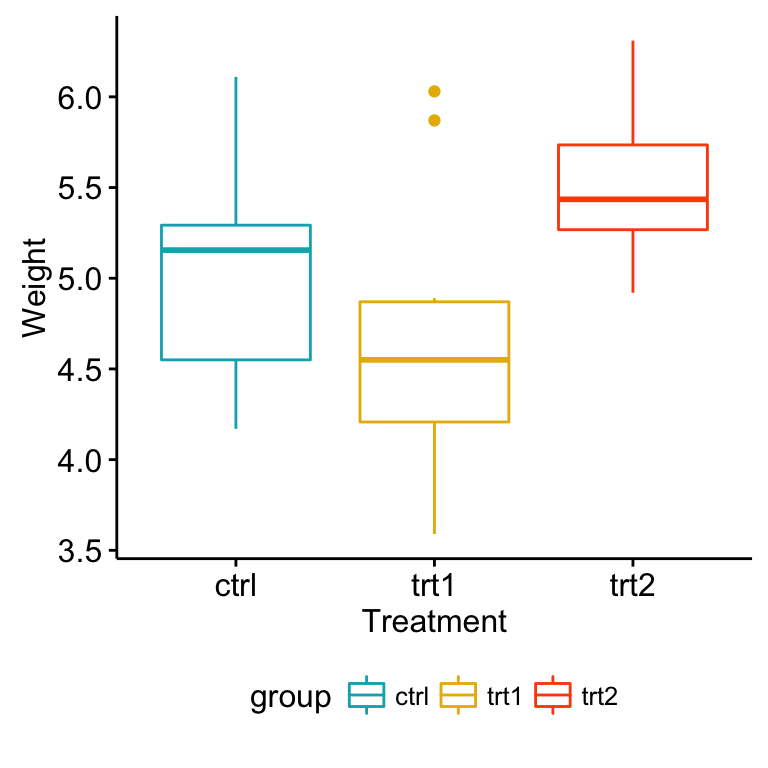

Kruskal-Wallis Test in R

# Mean plots
# ++++++++++++++++++++
# Plot weight by group
# Add error bars: mean_se
# (other values include: mean_sd, mean_ci, median_iqr, ....)
library("ggpubr")
ggline(my_data, x = "group", y = "weight", 
       add = c("mean_se", "jitter"), 
       order = c("ctrl", "trt1", "trt2"),
       ylab = "Weight", xlab = "Treatment")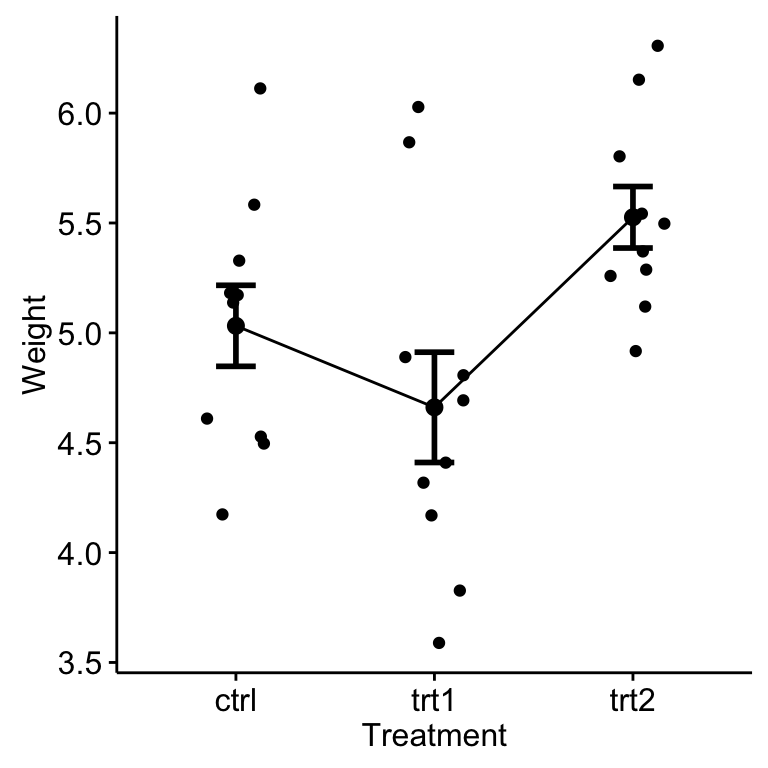

Kruskal-Wallis Test in R

Compute Kruskal-Wallis test

We want to know if there is any significant difference between the average weights of plants in the 3 experimental conditions.

The test can be performed using the function kruskal.test() as follow:

kruskal.test(weight ~ group, data = my_data)

    Kruskal-Wallis rank sum test
data:  weight by group
Kruskal-Wallis chi-squared = 7.9882, df = 2, p-value = 0.01842

Interpret

As the p-value is less than the significance level 0.05, we can conclude that there are significant differences between the treatment groups.

Multiple pairwise-comparison between groups

From the output of the Kruskal-Wallis test, we know that there is a significant difference between groups, but we don’t know which pairs of groups are different.

It’s possible to use the function pairwise.wilcox.test() to calculate pairwise comparisons between group levels with corrections for multiple testing.

pairwise.wilcox.test(PlantGrowth$weight, PlantGrowth$group,
                 p.adjust.method = "BH")

    Pairwise comparisons using Wilcoxon rank sum test 
data:  PlantGrowth$weight and PlantGrowth$group 
     ctrl  trt1 
trt1 0.199 -    
trt2 0.095 0.027
P value adjustment method: BH 

The pairwise comparison shows that, only trt1 and trt2 are significantly different (p < 0.05).